PRICE ELASTICITY OF DEMAND

Price elasticity of demand measures the responsiveness of demand to changes in the commodity’s own price. It represents the ratio of the relative change in a dependent variable (quantity demanded) to the relative change in an independent variable (Price).  Thus, price elasticity is the ratio of a relative change in quantity demanded to a relative change in price. Let ‘e’ stand for elasticity. Then  

  e_p = relative change in quantity demanded / relative change in price 

Also, elasticity measures percentage change in quantity demanded divided by the percentage in price.  Symbolically

  ep = percentage change in quantity demanded / relative change in price 
               

If percentages are known, the numerical value of elasticity can be calculated. The coefficient of elasticity of demand is a pure number i.e. it stands by itself, being independent of units of measurement. 

The coefficient of price elasticity of demand can be calculated with the help of the following formula.

                                                    ep= ∆Q/Q . P/ ∆P
where, Q is quantity, 
           P is price, 
          DQ/Q relative change in the quantity demanded, 
        P/∆P Relative change in price. 
A minus sign (-) is generally inserted in the formula before the fraction with a view to making the coefficient of elasticity a non-negative value. 
The price elasticity can be measured between two finite points on a demand curve (called arc elasticity) or on a point (called point elasticity).

Arc Elasticity: 

• Two finite points on a demand curve make an arc. 
• Arc elasticity is the average responsiveness to price changes shown by a demand curve over some definite stretch of the curve. 
• The measurement of elasticity of demand between any two finite points on a demand curve is known as arc elasticity. 

The elasticity coefficient can be calculated with the help of the following formula:                                  
                    ep= ∆Q/Q . P/ ∆P

For example, in the above Fig, two finite points R and S are taken to measure the arc elasticity. First we move to measure elasticity for a fall in the price of the commodity from Rs.40 to 20. DP is 40-20 = 20.  This decrease in price causes an increase in demand from 40 units to 70 so that DQ is 40-70 = -30. These values can be put in the formula so that
e_p=-30/20. 20/20                                                                            
This implies that a one percent fall in price of commodity X cause a 1.5 per cent increase in demand for X.

• The business executives need take adequate care in the measurement, interpretation and use of arc elasticity, as the elasticity coefficient may vary depending upon the direction of movement.
•  In this case we have measured the elasticity coefficient while moving down from point R to S. 
• The coefficient will be different while moving upward from S to R (increase in price from Rs.20 to 40 and quantity demanded is reduced from 70 to 40 giving an elasticity coefficient of  .42 implying that one per cent increase in price will reduce the quantity by.42 percent. 
• Thus the elasticity depends on the direction of change in price. Therefore, measuring elasticity through arc method, the direction of price change should be kept in mind. The way out of this difficulty is to take an average of prices and quantities and thus to measure elasticity at the midpoint of the arc. 

Linear demand curve showing point elasticity: Point elasticity is the ratio of an infinitesimally small relative change in quantity to an infinitesimally small change in price. If a price range is made as small as possible, that is, shrunk to a point- then the relative changes must be made as small as possible-infinitesimally small. Point elasticity is the ratio of an infinitesimally small relative change in quantity to an infinitesimally small change in price. 
Point elasticity of demand is defined as the proportionate change in the quantity demanded resulting from a very small proportionate change in price. Fig. shows how to find the elasticity at a point on a demand curve.            

 Let us take a point such as R on the demand curve DD. For measuring elasticity at a point the following formula may be used. e_p= ∆Q/Q . P/ ∆P.   Point elasticity is the product of price-quantity ratio (P/Q) at a particular point (R) on the demand curve (DD) and the reciprocal of the slope of the demand line. The slope of the demand slope is defined by RQ/QD. The reciprocal of the slope of the demand line is QD/RQ.

          P       = Q/ P = QD/RQ         
At point R, price P = RQ and Q = OQ

If we substitute these values in equation 3.11, what we get is   = RQ/OQ. QD/RQ = QD/OQ   If the numerical values for QD and OQ are available, elasticity at point R can be calculated. 
Price elasticity at Different Points on a Non-Linear Demand Curve: 
The method used to measure point elasticity on a linear demand curve cannot be applied straightway to measure point elasticity on a non-linear demand curve. 

In order to measure point elasticity on a non-linear demand curve, we first draw a tangent to the selected point and bring it on a linear demand curve. 
Fig illustrates how we can measure point elasticity on a non-linear demand curve at point R. For this purpose, we draw a tangent TT’ through point R. Since demand curve DD and the line TT’ pass through the same point R, the slope of the demand curve and that of the tangent is the same. Therefore, the elasticity of demand curve at point R will be the same as the elasticity on point R on line TT’. The formula applied to measure the elasticity on a linear demand curve can now be used as the non-linear demand curve has been changed into a linear demand curve.

                                                                    
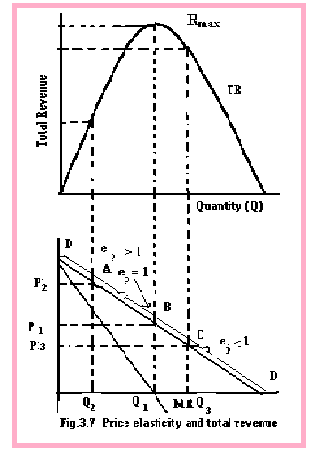
PRICE ELASTICITY AND TOTAL REVENUE

One important application of elasticity is to clarify whether a price increase will raise or lower total revenue. Many business executives are concerned with the issue whether it is worthwhile to raise prices and whether the higher prices make up for lower demand. Total revenue is equal to price times quantity (TR = P.Q). If we know the price elasticity of demand, we may know what will happen to total revenue when price changes: 

1.  If price elasticity (e_p > 1), reducing the price will increase the total revenue. 
2.  When demand is perfectly inelastic e_p = 0, there is no decrease in quantity demanded when price is raised. Therefore, a rise in price increases the total revenue and vice versa. 
3. In case of an inelastic demand (e _p  < 1), the total revenue falls when the price is decreased. The total revenue increases when the price is increased. 
4. When the demand for a product is unitary elastic (e_p = 1) quantity demanded increases or decreases in the proportion of increases or decrease in the price. 

Hence total revenue remains unaffected_. To make this point more clear, we require total and marginal revenue function and price-elasticity of demand  TR = P. The marginal revenue (MR) is the derivative of the TR function   
                         MR = Δ (TR)/ ΔQ = Δ (PQ)/ΔQ MR = P + Q.ΔP/DQ   
 If the demand curve is linear its equation is  
                                                               Q = b₀ – b₁ P. 
Solving for P,   P = a_{0 -} a₁Q. 
Where  a₀ = b₀/b₁, And a₁ = 1/b₁. 
Substituting P in the total revenue function we find. 
                                                    TR = PQ = a₀Q -a₁Q²                                            
The MR is the  MR = Δ (TR)/ΔQ = a₀ – 2a₁Q Figure shows that if the demand curve is falling the TR curve initially increases, reaches a maximum, and then commences declining. 
The relationship between MR, P and e can be used to establish the shape of the total-revenue curve.

The total revenue curve reaches its maximum level at the point where e_p = 1, because at this point its slope, the marginal revenue, is equal to zero

                                              MR = P (1 – 1/1) = 0

If e_p > 1 the total revenue curve has a positive slope. It is still increasing and has not reached its maximum point. If e_p <1 the total-revenue has a negative slope and is falling.

                                                          Fig.4     

The following can be summarized:

1.  If the e _p < 1), the demand is inelastic.  A rise in price causes an increase in total revenue, and a decrease in price leads to a fall in total revenue.
2.  If e _p > 1, the demand is elastic, and increase in price will cause a decrease in the total revenue and a decrease in price will lead to an increase in the total revenue.
3.  If e _p = 1, the demand is unitary elastic, total revenue is not affected by changes in price because MR has reached zero.

Price Elasticity and Marginal Revenue

Demand and marginal revenue curves show where demand is elastic, unitary elastic and inelastic. It is clear that demand becomes less elastic at lower prices. This is a characteristic of linear demand curves because the curve is linear dQ/dP is a constant. Thus price elasticity is determined by the value of P/Q. But as price decreases, P/Q also decreases

                                            

Consequently, the absolute value of e_p becomes smaller and demand becomes less elastic.

The above figure illustrates that the point of unitary elasticity corresponds to the point where the marginal revenue crosses the quantity axis. 

• The marginal revenue is zero where demand is unitary elastic. 
• Unitary elasticity means that a 1 percent increase in price causes quantity demanded to decrease by 1 percent and the increase in price is exactly offset by the decrease in quantity demanded. Consequently, there is no change in total revenue as the marginal revenue is zero.
• The marginal revenue is positive where demand is elastic and negative when demand is inelastic. Note that these relationships are also true for nonlinear demand curves. The point where marginal revenue is zero always divides the elastic and inelastic regions of the demand curve.

 In case of a vertical demand curve, quantity demanded is not affected by changes in price as dQ/dP is zero and price-elasticity is also zero. For a horizontal demand curve, quantity demanded is highly responsive to changes in price as even a very small change in price can lead to an infinitely large change in quantity demanded as dQ/dP and price elasticity being infinite. Horizontal demand curves are said to be infinitely elastic. The cases of infinitely elastic or completely inelastic demand curves are rare to find in real life, but an understanding of these is useful for economic analysis.